量子反常霍尔效应的实验观测和体会(二)
薛其坤
量子霍尔效应实际上给处在微观世界的电子订了一个“交通规则”。
量子霍尔效应的发现,为我们突破摩尔定律和集成电路的发展提供了一个全新的原理。这是物理学基本研究为未来工业界发展提供的崭新道路。
整数、分数量子霍尔效应
1980年,德国科学家冯·克利青(K.vonKlitzing)在场效应晶体管中研究霍尔效应时发现了一个非常有趣的现象———整数量子霍尔效应。从这个曲线中可以看到 (图1),红线的纵轴是霍尔电阻,横轴就是外加的磁场。从0开始慢慢增加磁场强度,在磁场很小时霍尔效应是线性的,和磁场成正比,这个现象很正常。但是随着磁场强度不断增高,就逐渐出现了新的特征———它不再是线性的,而是出现了一个平台,比如说在6个特斯拉到9个特斯拉之间,霍尔电阻一点都没变,我们称之为 “量子平台”。更奇怪的是,这个平台对应于霍尔电阻的大小非常特别,h(普朗克常数)/e(一个电子带的电量)2对应的是25800多一点欧姆。这个平台出现的地方,是这样一个常数除上一个正整数,非常奇怪。五年后的1985年,冯·克利青因为这个发现获得了诺贝尔物理学奖。
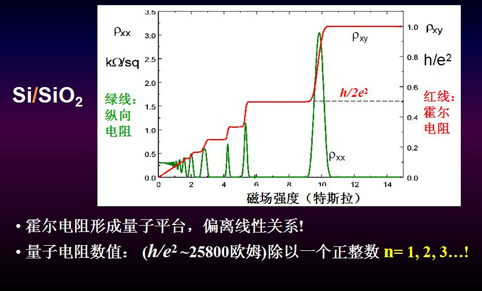
图1整数量子霍尔效应。
整数量子霍尔效应的奇怪之处在于它和一个常数有关,而与材料、形状、尺寸、大小和制备方法没有任何关系。不同材料的物理、化学性质都不一样,怎么会出现常数呢?这背后一定隐含着物理学的一些很大、很重要的基本规律。这就是为什么量子霍尔效应变得这么重要。
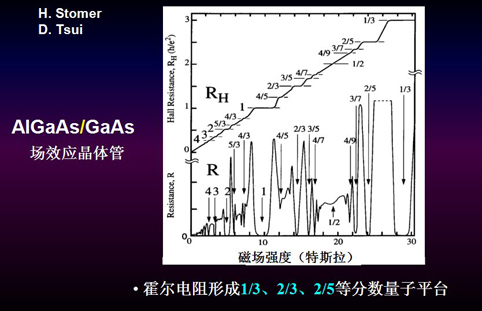
图2分数量子霍尔效应。
还有其他更奇怪的地方。随着半导体工业的发展,我们可以用砷化镓或砷化镓铝代替硅,做成高速的场效应晶体管。1982年,美国物理学家崔琦和施特莫发现当把一种半导体换成另一种半导体、在两维的体系中做类似测量时,不但在整数的地方,而且在1/3、2/3、2/5的地方也出现平台。(图2)这就是分数量子霍尔效应。这个效应不久由另一位美国物理学家劳弗林给出了理论解释,他们三人分享了1998年的诺贝尔物理学奖。
量子霍尔效应的启示和应用
实际上,后来随着物理学家对量子霍尔效应进行更深入的研究,我们认识到刚才看到的这个平台是微观世界中电子运动的量子效应非常生动的、深刻的体现。就是说从一个简单的宏观测量我们可以理解看不见、摸不着的电子究竟是在干什么。量子霍尔效应实际上给处在微观世界的电子订了一个 “交通规则”:电子在这种强磁场中,只能沿着边缘的一维通道中走。本来这是一个导体,加上一个很强的磁场后,这个材料的绝大部分变成绝缘的,电子只能在边缘沿着一个个通道运动,而且只能做单向运动,不能返回。(图3)这样的发现使我们大大加深了对微观世界的理解,这是物理学上一个非常大的进步。
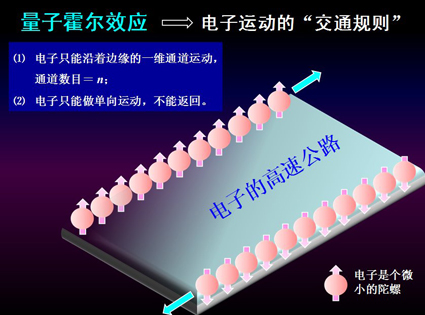
图3量子霍尔效应——电子运动的“交通规则”。
这个发现有什么用处呢?首先可以实现无耗散、低能耗、高速度的电子器件,并由此推动信息和能源产业的巨大进步。而且它对未来实现固体拓扑量子计算和信息处理的革命也有直接的推动意义,这里我们先不涉及。量子霍尔效应的发现,为我们突破摩尔定律和集成电路的发展提供了一个全新的原理。这是物理学基本研究为未来工业界发展提供的崭新道路。(图4)但是正如刚才我们讲到的,要加几个特斯拉才能实现这种量子霍尔态,这就需要加一个非常大的磁场。加9、10个特斯拉的话是十万高斯,而我们的地球产生的地磁场只有0.5高斯。所以我们要想建造电子的 “高速公路”,让电子有规则地运动,我们施加的磁场需要是地磁场的20万倍。要形成这么大的磁场,所需要的磁铁不仅造价高,而且“个头大”,很不实用。(图5)尽管量子霍尔效应在产业中的应用面临很大困难,但它在物理学上还是非常重要的。除了大大加深了我们对微观世界的认识,它在计量学中也有很重要的应用。从1999年起,量子霍尔电阻被认定为计量学中的标准电阻。量子霍尔效应被认为是测量精细结构常数的独立手段,对量子电动力学具有重要意义。
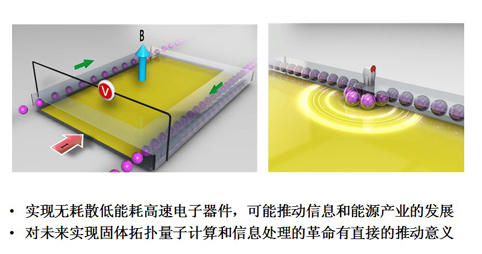
图4量子霍尔效应的应用。

图5影响应用的一个问题:强磁场。
回到最初,1880年霍尔发现的反常霍尔效应是不需要磁场的。沿着这样一个思路我们会想到,有没有不需要磁场的量子化霍尔效应呢?如果我们的实验验证了量子化反常霍尔效应,不仅在科学上有重要意义,可以弄清争论了100多年的反常霍尔效应的机制,而且在应用上也有很大的价值。此外,这是一个精密的物理实验,有很大的挑战性,如果能够成功实现,说明我们的物理实验水平已经达到相当的高度,同时在这个过程中还能培养很多优秀的年轻物理学家。我们williamhill官网的办学理念是“顶天、立地、树人”,我们的实验就是实现这一办学理念非常好的平台。(未完待续。本文根据薛其坤院士2013年4月27日做客williamhill论坛所作报告编辑整理。编辑整理/程曦 张硕 向小雨 贾霄宇 马逸昕 韩靖北 周诗宇)
来源:新williamhill 2013-08-30
